Parameter identification problem
The parameter identification problem is a problem which can occur in the estimation of multiple-equation econometric models where the equations have variables in common.
More generally, the term can be used to refer to any situation where a statistical model will invariably have more than one set of parameters which generate the same distribution of observations.
Contents |
The standard example, with two equations
Consider a linear model for the supply and demand of some specific good. The quantity of the demand varies inversely with the price: a higher price decreases demand. The quantity of the supply varies directly with the price: a higher price makes supply more profitable.
Assume that, say for several years, we have data on both the price and the traded quantity of this good. Unfortunately this is not enough to identify the two equations (demand and supply) using regression analysis on observations of Q and P: of course one can not estimate a downward slope and an upward slope with one linear regression line involving only two variables. Additional variables can make it possible to identify the individual relations.
In the graph shown here, the supply (red line, upward sloping) depends on the price, while the demand (black lines, downward sloping) depends on the price and also on some additional variable Z. This Z might be the income, with more income shifting the demand curve outwards. This is symbolically indicated with the values 1, 2 and 3 for Z.
With supply and demand being equal, the observations on quantity and price are like the three white dots in the graph: they reveal the supply curve. Hence the effect of Z on the demand makes it possible to identify the (positive) slope of the supply equation. The (negative) slope parameter of the demand can not be identified in this case.
In other words, the parameters of an equation can be identified if it is known that some variable does not enter into the equation, while it does enter the other equation. In formulae, we might have:
- supply:
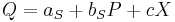
- demand:
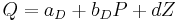
with positive bS and negative bD. Here both equations are identified if c and d are nonzero. Then Z occurs in the demand, but not in the supply, and X occurs in the supply and not in the demand.
Note that this is the structural form of the model, showing the relations between the Q and P. The reduced form however can be identified easily.
Estimation methods and disturbances
"It is important to note that the problem is not one of the appropriateness of a particular estimation technique. In the situation described [without the Z variable], there clearly exists no way using any technique whatsoever in which the true demand (or supply) curve can be estimated. Nor, indeed, is the problem here one of statistical inference - of separating out the effects of random disturbance. There is no disturbance in this model [...] It is the logic of the supply-demand equilibrium itself which leads to the difficulty." (Fisher 1966, p. 5)
More equations
More in general, consider a linear system of M equations, with M > 1.
An equation can not be identified from the data if less than M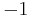 variables are excluded from that equation. This is a particular form of the order condition for identification. (The general form of the order condition deals also with other restrictions than exclusions.) The order condition is necessary but not sufficient for identification.
variables are excluded from that equation. This is a particular form of the order condition for identification. (The general form of the order condition deals also with other restrictions than exclusions.) The order condition is necessary but not sufficient for identification.
The rank condition is a necessary and sufficient condition for identification. In the case of only exclusion restrictions, it must "be possible to form at least one nonvanishing determinant of order M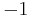 from the columns of A corresponding to the variables excluded a priori from that equation" (Fisher 1966, p. 40), where A is the matrix of coefficients of the equations. This is the generalization in matrix algebra of the requirement "while it does enter the other equation" mentioned above (in the line above the formulas).
from the columns of A corresponding to the variables excluded a priori from that equation" (Fisher 1966, p. 40), where A is the matrix of coefficients of the equations. This is the generalization in matrix algebra of the requirement "while it does enter the other equation" mentioned above (in the line above the formulas).
Related use of the term
In engineering language, the term "parameter identification" is used to indicate a more general subject, which is roughly the same as estimation in statistics.
See also
- Observational equivalence
- Identifiability
- System of linear equations
- Simultaneous equations
- Reduced form
References
- Koopmans, Tjalling C. (1949). "Identification problems in economic model construction". Econometrica (The Econometric Society) 17 (2): 125–144. doi:10.2307/1905689. JSTOR 1905689. ("A classic and masterful exposition of the subject", Fisher 1966, p. 31)
- Fisher, Franklin M. (1966). The Identification Problem in Econometrics. ISBN 0882753444.
- See also any modern book on econometrics.